Корпус Применение труб в газовых скважинах высокотемпературных

Свойства оцинкованных стальных труб Приваривать

январь 4, 2019

Коррозионная стойкость API 5L Pipeline стали с защитным покрытием

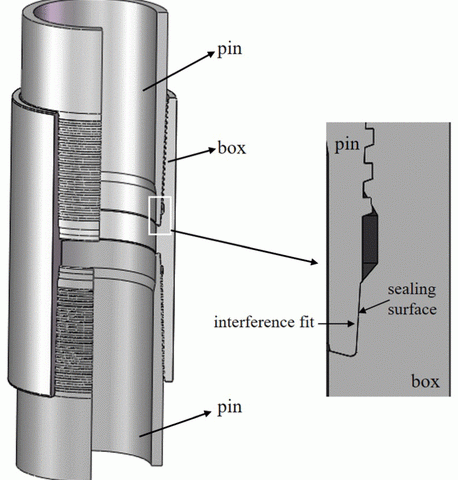
январь 7, 2019

В былые времена, с уменьшением числа легко эксплуатируемых нефтяных и газовых скважин, это стало необходимым для нефтяных и газовых скважин углубиться на обоих подземных и подводных. А также, НКТ и обсадные струны подвергаются более высокой температуре и высоком давлении в этих скважинах, который, вероятно, привести к повреждению корпуса или утечки газа в высоком давлении / высокой температуре (НРНТ) углубления. Таким образом, больше внимания уделяется скважинным целостности в нефтяной и газовой промышленности в последнее время years.1,2 Ключевым фактором целостности ствола скважины обсадной колонны соединения, которые, как ожидается, чтобы обеспечить как структурную и утечки целостность при неблагоприятных условиях окружающей среды. Поскольку условия погрузки связаны с глубже, более высокие температуры и давления газовых скважин, многие операторы перешли от использования стандартного Американского нефтяного института (API) Соединения с премиальными резьбовыми соединениями.Тем временем 1 показывает корпус премиальных соединений и его уплотняющего газа механизма. Уплотнительная поверхность также называют металл-металл уплотнения, которые обеспечивают контактное давление через натяг. Больше того, контактное давление на уплотняющей поверхности выше, чем давление газовой скважины, и соединения обсадных труб может предотвратить утечку газа efficiently.3,4

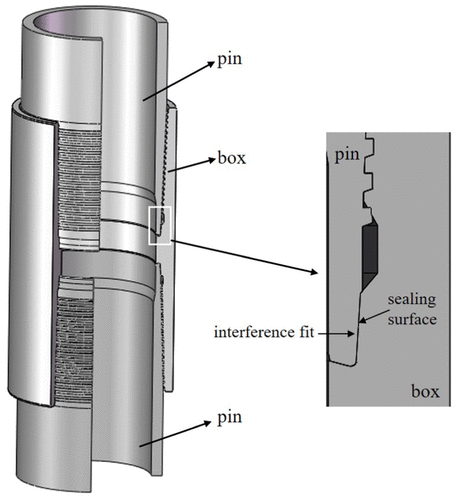
Тем временем 1. уплотняющий газ механизм премиум связи.

В былые времена, соединение газового уплотнения не удалось в некоторых дополнительных-высокая температура газовая скважина, хотя проектирование контактное давление на уплотняющей поверхности была выше, чем давление газа. В Южном Китае Море, температура в некоторых разведочных газовых скважинах может достигать до 240 ° С.5 хорошо разработанных премиальных соединений может иметь газа высокого давления в скважине на ранней стадии. тем не мение, проблема утечки газа может быть обнаружена после 2 лет добычи газа в некоторых скважинах, что гораздо меньше, чем ожидаемый срок службы газовых скважин. В экстра-высоких температурах, уплотнительная поверхность соединений обсадных будет испытывать ползучести при растяжении, что приведет к снижению контактного давления уплотнительной поверхности в. Когда контактное давление ниже, чем давление газовой скважины, газ будет вытекать из соединения корпуса, что позволит сократить срок службы газовой скважины. более того, это принесет устойчивое давление попутного газа, смятие обсадной колонны, или оставление хорошо, вызывая огромный экономический ущерб. Следовательно, это имеет большое значение для изучения вязкоупругости материала соединительного обсадной колонны и выяснить релаксацию контактного давления на поверхности уплотняющей, которые могут быть полезны для разведки и разработки газовых скважин высокотемпературных.

Исследования на соединениях обсадных были в основном сосредоточены на проектировании и безопасности оценки структуры резьбовое соединение в последние годы. Аналитический метод,6,7 заключительный элемент (FE) метод,8,9 и экспериментальные method10,11 были широко приняты в научно-исследовательских работах. Некоторые исследователи исследовали уплотнительный механизм премиальных соединений,12,13 и некоторые исследователи разработали соединение премиума высокой производительности в высокотемпературном / высоком давлении (HTHP) газ well.14,15However, эти исследовательские работы проводятся все в стационарном состоянии, не считая времени меняющийся. А также, уплотнительный механизм премиальных соединений в скважине высокотемпературного газа не был полностью исследован, особенно вязкоупругого поведения материала оболочки.

В этой статье, Эксперимент ползучести материала оболочки проводили при том же напряжении растяжения, но с разными температурами. А потом, поведение вязкоупругого материала оболочки изучается. более того, WLF (Уильям-Landel-Ферри) Уравнение для материала оболочки происходит. в заключение, модель FE используется для изучения релаксации контактного давления уплотняющей поверхности в соединении корпуса, который может предсказать его срок службы в скважине высокотемпературного газа.

Экспериментальные испытания материалов

Экспериментальная установка и методика

В соответствии с ISO 204:2009, одноосное испытание ползучести металлических материалов в способе натяжения теста, Эксперименты выполнены на ползучесть при различных высоких температурах, чтобы оценить материал релаксации механических свойств, основанные на теории viscoelasticity.16 Как показаны в Тем временем 2, устройство ползучести эксперимент состоит из печи, Датчик температуры, сеньор смещение, Испытательное напряжение, и образец. Принцип эксперимента показан на Тем временем 2(b). Нижняя часть образца фиксируется, и вершина загружается. Экспериментальная температура контролируется печи и датчиком температуры. Тем временем, деформация ползучести регистрируется датчиком смещения. Материал образца Корпус P110T и его химический состав приведен в таблице 1. В качестве эксперимента металла ползучести отнимает много времени, набор испытаний под нагрузкой постоянного натяжения проводит при температуре 120 ° C, 200° C, и 300 & deg; С, соответственно.

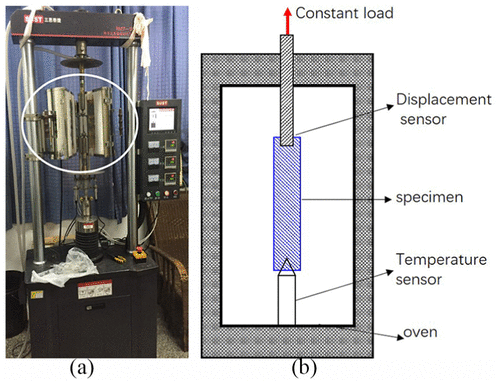
Тем временем 2. (Стандарты — это повторяющиеся вещи с характеристиками, связанными с разнообразием, в экономической и технологической деятельности.) Ползучесть эксперимент приборы и (b) экспериментальный принцип.

Экспериментальный результат

Таблица 2 показывает условия ползучести экспериментальные, которые включают в себя постоянную нагрузку натяжения 680 МПа, три различных температуры, и потребляя время эксперимента. Кроме того, загруженное растягивающее напряжение находится под пределом упругости материала P110T. В тесте #1, образец был нарушен после 570 ч эксперимента при 300 ° C, как показано в Тем временем 3. Это показывает, что разрушение образца относится к явлениям утонения. тем не мение, при более низкой температуре и после 630 ч испытаний на ползучесть, образец не сломаться. Это доказывает, что поведение материала ползучести при 300 ° C более очевидно, чем при более низких температурах. Результаты ползучести эксперимента показаны на Тем временем 4. Штамм времени кривой на 300 ° С состоит из целых трех стадий ползучести: первичный, вторичный, и третичный. А также, скорость деформации определяется как отношение напряжения к тому времени,. В начальной стадии, скорость деформации относительно высока, но замедляется со временем. Бесшовная труба, скорость деформации в конце концов, достигает минимальное значение и становится постоянным при вторичном этапе, в качестве кривой деформации времени представляет собой прямую линию, на данном этапе. в заключение, в третичной стадии, скорость деформации в геометрической прогрессии не увеличивается со временем до тех пор, трещин образца, что в основном обусловлено сужением явления в образце. тем не мение, для образца при температуре 120 ° C и 200 ° C ползучести эксперимента, были только два этапа во время 630 тестирования часов: начальная стадия и вторичная стадия.

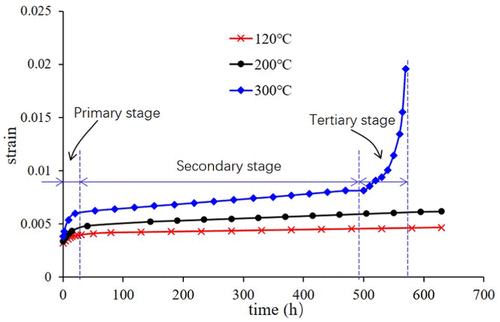
Тем временем 4. Ползучесть результатов эксперимента при различной температуре.

Вязкоупругая конститутивная модель

В этой статье, материал корпуса выбран в качестве линейной вязкоупругой. Материальные отношения могут быть выражены линейным принципом суперпозиции вязкоупругость и использование релаксации и ползучести модуля упругости function.17,18 Начиная с обобщенной модели Максвелла и добавив еще один член пружины приводит к модели, известной как модель вихертовского, в соответствии с Тем временем 5. Используя модель Вихерта, ползучести и релаксации вязкоупругого материала могут быть описаны хорошо, и эта модель может быть представлена с помощью функции модуля релаксации E(t) следующее

E (t) = E_{\infty} + \sum_{i = 1}^{n} E_{i} \exp (\frac{- t}{τ_{i}})

(1)

где $τ_{i}$ время релаксации, $E_{i}$ это модуль релаксации, $E_{\infty}$ равновесное модуль, и п общее число членов ряда Прони. Уравнение (1) представляет собой сумму ряда экспоненциальных членов и может быть интерпретирован как механический элемент модель, также известный как серия Прони.

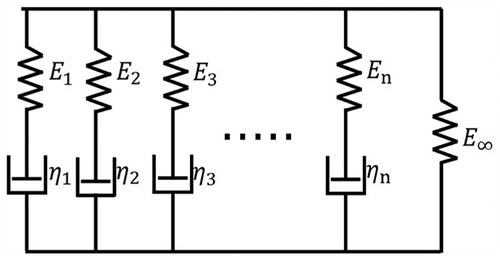
Тем временем 5. Режим ВИХЕРТ материала.

Обратите внимание, что, из уравнения (1), Если T = 0

E (0) = E_{0} = E_{\infty} + \sum E_{i}

(2)

где E0 мгновенна модуль релаксации. А также, уравнение (1) можно переписать следующим образом

E (t) = E_{\infty} + \sum_{i = 1}^{n} m_{i} E_{0} \exp (\frac{- t}{τ_{i}})

(3)

где $m_{i} = E_{i} / E_{0}$ определяется как параметр серии Прони.

P110T материал характеристика

Что касается эксперимента ползучести, нагрузка натяжения приложения является постоянной, и модуль релаксации может быть представлен другой формой

E (t) = \frac{σ}{[ε]}

(4)

где $σ$ это растягивающая нагрузка приложения; $[ε]$ является матрицей деформации для эксперимента ползучести, $[ε_{1}, ε_{2}, ε_{3}, \dots]$ , соответствующий временной матрицы эксперимента $[t]$ или же $[t_{1}, t_{2}, t_{3}, \dots]$ . Таким образом, модуль упругости Е релаксации(t) в матричной форме

E (t) = E_{0} + \sum_{i = 1}^{n} m_{i} E_{0} [1 - \exp (\frac{[t]}{τ_{i}})]

(5)

Комбинируя уравнения (4) с уравнением (5), соотношение между временем и деформации устанавливается, как показано в уравнении (6)

\sum_{i = 1}^{n} m_{i} E_{0} [1 - \exp (- \frac{[t]}{τ_{i}})] = E_{0} - \frac{σ}{[ε]}

(6)

По решению уравнения (6) метод линейного матричного уравнения и подставив временную матрицу $[t]$ и матрица деформации $[ε]$ с использованием экспериментальных данных ползучести, параметр серии Прони ми может быть получен.

Что касается вычислительной сложности функции серии Прони, программное обеспечение MATLAB применяется, чтобы найти параметр серии Прони. Для 200 ° C температуры окружающей среды, параметр серии Прони материала P110T обсадной колонны приведены в таблице 3, и его модуль релаксации уравнение можно получить следующим образом

\begin{matrix} E (t) = 79, 827 + 61, 991 [1 - e^{\frac{- t}{10}}] \\ + 7367 [1 - e^{\frac{- t}{100}}] + 49, 615 [1 - e^{\frac{- t}{1000}}] \end{matrix}

Согласно теории Гука закон, деформация ползучести представляет собой отношение постоянного натяжения напряжения к модулю релаксации E(t). Кроме того, отношение кривой деформации ползучести в зависимости от времени показана на Тем временем 6. По сравнению с штаммом-кривое время в эксперименте приводит при 200 ° C, как показано в Тем временем 6, модель серии кривой Прони хорошо согласуется с экспериментальными данными ползучести, который проверки конститутивной модели P110T материала. Следовательно, серия уравнение Прони из материала корпуса P110T при 120 ° C и 300 ° C могут быть также получены таким же образом,, как показано в уравнениях (8) а также (9), соответственно

\begin{matrix} E (t) = 125, 986 + 875 [1 - e^{- t}] + 43, 314 [1 - e^{\frac{- t}{12}}] \\ + 2956 [1 - e^{\frac{- t}{100}}] + 38, 942 [1 - e^{\frac{- t}{1000}}] \end{matrix}

(8)

\begin{matrix} E (t) = 53, 560 + 66, 362 [1 - e^{\frac{- t}{5}}] + 6985 [1 - e^{\frac{- t}{10}}] \\ + 4802 [1 - e^{\frac{- t}{200}}] + 30, 015 [1 - e^{\frac{- t}{800}}] \end{matrix}

(9)

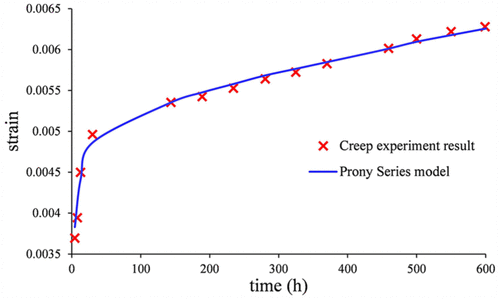
Тем временем 6. Ползучесть экспериментальные данные и прочность на разрыв серии Прони в сравнении со скоростью 200 & deg; С.

Термо-реологические свойства материала оболочки

Модуль релаксации от температуры dependent.19,20 При более низких температурах, скорость релаксации материала является очень медленным, который может быть смоделирована как упругое поведение. При более высоких температурах, скорость релаксации материала становится намного быстрее, который является чистым вязким поведением. Модуль релаксации, полученный методом серии Прони, нанесен на временной шкале журнала в рамках трех различных температур, как показано в Тем временем 7. Его можно найти, что все участки имеют почти одинаковую форму, но лишь смещаются по горизонтали. Это свойство материала оболочки и называется термо-реологические свойства. Среднее значение горизонтального расстояния между двумя кривыми, на вершине, средний, и снизу, определяется как фактор сдвига, $α_{T}$ , и соотношение между кривыми можно описать следующим уравнением

E (\log (t), T) = E (\log (t) - \log α_{T}, T_{1})

(10)

где E(t, T) это модуль релаксации при температуре Т и время Т.

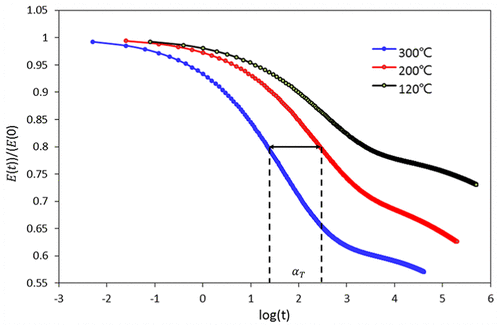
Тем временем 7. Термо-реологические свойства материала оболочки P110T.

Уравнение (10) можно переписать следующим образом

E (t, T) = E (\frac{t}{α_{T}}, T_{1})

(11)

Фактор сдвига $α_{T}$ может быть получено с помощью уравнения WLF

\log α_{T} = - \frac{C_{1} (T - T_{0})}{C_{2} + (T - T_{0})}

(12)

где Т представляет собой температуру, при которой рассчитывается модуль релаксации, $T_{0}$ является эталонной температурой. C1 и C2 константы уравнения WLF.

На основе экспериментальных данных ползучести и метода Прони в серии Тем временем 6, и установка 200 ° C в качестве эталонной температуры, факторы сдвига, от 200 ° C до 120 ° C и 200 ° C до 300 ° C, можно масштабировать на участке. Подставляя факторы сдвига в уравнении WLF, константы C1 и C2 могут быть решены: С1 = 45,03 и С2 = 4640. Следовательно, уравнение ВЛФ для материала оболочки P110T является

\log α_{T} = - \frac{45.03 (T - 200)}{4640 + (T - 200)}

(13)

моделирование FE и его применение

модель FE

Численное моделирование испытания образца напряжения ползучести проводили с использованием коммерческого программного обеспечения FE ABAQUS. На основе материал корпуса P110T ползучесть эксперимент загрузки, была установлена механическая модель FE, как показано в Тем временем 8. Упругие свойства, в том числе модуля упругости и коэффициента Пуассона, 1.99× 105 МПа и 0.3, соответственно, определены в ABAQUS. Кроме того, вязкие свойства, включая время релаксации и серию Прони, как показано в таблице 3, также определены в ABAQUS. Больше того, термо-реологической простой (ТРС) параметры, C1 и C2, получено уравнение WLF, также включены в этой симуляции, и * VISCO тип анализа был применен для вязкоупругого поведения.

Тем временем 8. FE механическая модель, используемая для моделирования испытания на растяжение ползучести.

Сравнение ползучести экспериментальных данных и результатов моделирования при трех различных температурах показано в Тем временем 9(Стандарты — это повторяющиеся вещи с характеристиками, связанными с разнообразием, в экономической и технологической деятельности.)–(c), соответственно. При температуре 200 ° С, результат моделирования соответствует ползучести экспериментальных данных. Это происходит потому, что температура 200 ° С было установлено в качестве опорной температуры в уравнении (13). Но для температур 120 ° С и 300 ° С, а термо-реологическим поведением, Есть небольшие различия между экспериментальным и результатами моделирования, и самая большая разница меньше 8%. Причина этого различия, потому что это, для анализа FE, термо-реологических параметров применяются в моделировании, которое получается из уравнения WLF. В уравнении WLF, 200 ° С принимается в качестве опорной температуры, чтобы, в Тем временем 7, красная кривая сдвигается в положение синей кривой и черной кривой. А также, новые сдвинутые кривые представляют термо-реологическое поведение материала оболочки и используются для решения уравнения WLF. Поскольку сдвинутые кривые не могут 100% хорошо согласуются с исходной, который получен экспериментальные результаты, отклонение существует между экспериментальной и моделирования. Кроме того, как 200 ° С берется в качестве эталонной температуры, результат моделирования является более точным, чем другие, как показано в Тем временем 9. Следовательно, Результаты моделирования показывают обоснованность теории вязкоупругих и метода ТРС в этой статье. К тому же, модель ИПА может быть использована для оценки вязкоупругого поведения материала корпуса P110T при различных механических и термических условиях.

Тем временем 9. Сравнение экспериментальных данных и моделирования результата при различных температурах: (Стандарты — это повторяющиеся вещи с характеристиками, связанными с разнообразием, в экономической и технологической деятельности.) 120° C, (b) 200° C, а также (c) 300° C.

Контакт давление на уплотняющей поверхности

На основе геометрии 5.5 SL-APOX совместного типа соединения ", осевая симметрия FE модель для уплотняющей поверхности была построена в ABAQUS, как показано в Тем временем 10. Внутренняя стенка находится под действием приложенного давления газа. Красная линия на рисунке представляет собой уплотняющую поверхность. Если давление газа выше, чем контактное давление на уплотняющей поверхности, совместное подключение будет больше шансов просочиться.

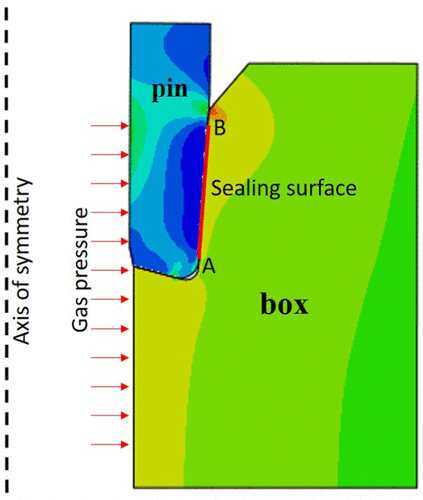
Тем временем 10. Метод конечных элементов модели уплотнительной поверхности от шарнирного соединения SL-APOX.

При высокой температуре окружающей среды-, контактное давление на уплотняющей поверхности будет уменьшаться со временем из-за материал вязкоупругости. Давление газа на внутренней стенке установлено до 75 МПа. Результат моделирования усредненной релаксации контактного давления на уплотнительной поверхности в зависимости от времени показан на Тем временем 11. Результаты моделирования показывают, что начальное среднее контактное давление составляет 116 МПа при температуре 160 ° С и 230 ° С. Бесшовная труба, среднее давление контакта уменьшается со временем. Среднее давление контакта падает до 76 МПа. более того, скорость уменьшения давления при 230 ° С происходит быстрее, чем тот, при 160 ° C окружающей среды. Показано, что в течение 4000 ч (166дней), контактное давление падает до 76 МПа при температуре 230 ° C. тем не мение, при более низкой температуре окружающей среды, это займет 9000 ч (375дней) снизится до 76 МПа.

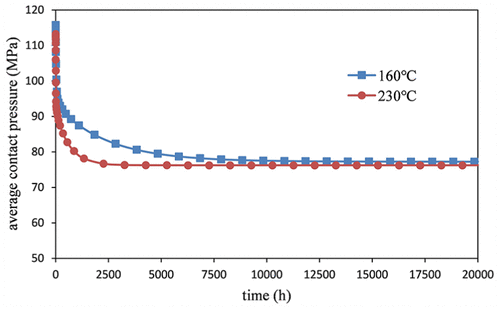
Тем временем 11. Расслабление контактного давления на поверхности уплотнительного изменения со временем.

Согласно результатам моделирования, отношение начального контактного давления и давление флерона контакта 1.56, что значит, при высокой температуре окружающей среды-, конечный контактное давление на уплотняющей поверхности упадет почти на треть. Основываясь на уравнении коэффициента запаса

n = \frac{[σ]}{σ_{gp}}

(14)

где п фактор безопасности, $[σ]$ является проектирование контактного давления, $σ_{gp}$ это намерение уплотнения давление газа. Коэффициент безопасности п должно быть больше 2 для рассмотрения безопасности.

Заключение

Релаксациями контактного давления на уплотнительной поверхности соединения премиума является основной причиной утечки газа из корпуса при высокотемпературной скважине природного газа.
При высоких температурах, ползучести эксперимент напряжения был использован для изучения поведения вязкоупругого материала в корпус P110T. Механическое поведение материала оболочки сильно зависит от температуры. Чем выше температура окружающей среды является, тем быстрее скорость ползучести.
Конститутивная модель для материала оболочки P110T была получена с помощью экспериментальных данных ползучести, а параметр серии Прони был рассчитан. Термо-реологическое поведение также было исследовано, и сдвиг факторы окружающей среды материала между температурой 120 ° C до 300 ° C, получают.
Была создана вязкоупругого FE модель для материала P110T, и результаты моделирования хорошо согласуются с экспериментальными данными.
Модель FE уплотнительной поверхности в премиальных соединениях была построена в ABAQUS, и его релаксация контактного давления была исследована. Рекомендуется, чтобы проектирование контактное давление на уплотняющей поверхности должно быть вдвое больше, вступающих давление уплотнительного газа при высокотемпературных газовых скважин.

Работа с редактором: Михал Kuciej

Декларация конфликтующих интересов
Автор(s) не заявил ни одного потенциального конфликта интересов в отношении исследований, авторство, и / или публикация этой статьи.